내 맘대로 프로그램 설계 6. - 데이터구조와 알고리즘.
내 맘대로 하는 프로그램 설계 시리즈.
Chapter1 - 간단한 데이터 처리(4섹션)
2017/12/27 - [프로그래밍/설계] - 내 맘대로 프로그램 설계 1. - 이유와 준비.
2018/01/11 - [프로그래밍/설계] - 내 맘대로 프로그램 설계 2. - 데이터 타입.
2018/01/16 - [프로그래밍/설계] - 내 맘대로 프로그램 설계 3. - 함수와 변수.
2018/05/29 - [프로그래밍/설계] - 내 맘대로 프로그램 설계 4. - 고정 크기 데이터.
2017/06/30 - [프로그래밍/설계] - 프로그래밍과 추상화에 대하여.[부록]
Chapter2 - 임의의 데이터 처리
2018/06/10 - [프로그래밍/설계] - 내 맘대로 프로그램 설계 5. - 리스트와 재귀.
2019/05/20 - [프로그래밍/설계] - 내 맘대로 프로그램 설계 6. - 데이터구조와 알고리즘(현재).
Chapter3 - 추상화
2019/05/20 - [프로그래밍/설계] - 내 맘대로 프로그램 설계 7. - 함수형 프로그래밍.
1. 시작.
리스트와 재귀를 배웠으니 본격적으로 자료구조를 배워보도록 합시다.
자료구조는 자료에 대해 효율적으로 접근하고 수정하기 위해 만들어진 개념입니다.
모든 물건을 집에 늘어놓고 쓰는 것이 아니라 책장, 서랍, 상자등에 보관하면 보기에 깔끔한 것이 아니라 찾기에도 편하잖아요??
자료구조는 책장, 서랍, 상자처럼 데이터를 깔끔하게 묶어주고 빠르고 편하게 사용할 수 있도록 도와줍니다.
자료구조 중 가장 기초적인 형태는 링크드 리스트(Linked List)입니다.

링크드 리스트(Linked List) [from Wikipedia)
전 시간에 다루었던 리스트와 유사하죠??
사실 링크드 리스트를 구현하려면 전 리스트와 후 리스트를 연결하는 과정에서 'C언어의 포인터' 개념이 필요한데..
포인터는 초보자들이 다루기 어려운걸로 유명합니다.
이하 각 리스트는 노드(Node)라 부르도록 합시다.
따라서 자료구조의 개념을 잡는 것이 아니라 컴퓨터구조에 대해 공부해야하는 목적과 수단이 역전되는 상황이 나오기도 합니다.
리스트를 기본적으로 제공하는 것은 제가 Racket이라는 언어를 고른 이유들 중 하나입니다.
Racket이 리스트를 대상으로 제공하는 4가지의 연산을 알아볼까요?
Code 6.1
(length '(1 2 3 4 5))
(reverse '(1 2 3 4 5))
(list-ref '(1 2 3 4 5) 2)
(append '(1 2 3) '(4 5))결과: 5, (list 5 4 3 2 1), 3, (list 1 2 3 4 5)
각각 리스트의 크기(길이), 거꾸로된 리스트, 3번째 값(0부터 시작), 합쳐진 리스트를 반환합니다.
그럼 위의 함수를 활용하든, 재귀를 사용하든 마지막 노드 값을 반환하는 함수를 짜봅시다.
Code 6.2
;;last-node: list -> node
;;Return list's last element
(define (last-node1 list)
(car (reverse list)))
(define (last-node2 list)
(list-ref list (- (length list) 1)))
(define (last-node3 list)
(if (zero? (length (cdr list)))
(car list)
(last-node3 (cdr list))))
(define (last-node4 list)
(if (null? (cdr list))
(car list)
(last-node4 (cdr list))))
(check-expect (last-node1 '(1 2 3 4 5)) 5)
(check-expect (last-node2 '(1 2 3 4 5)) 5)
(check-expect (last-node3 '(1 2 3 4 5)) 5)
(check-expect (last-node4 '(1 2 3 4 5)) 5)결과: 모든 4개 테스트 통과함!
일부로 다양한 방식을 보여주고 싶어서 4가지 방식으로 구현해봤습니다.
- 1번째는 리스트를 거꾸로 뒤집고, 첫번째 노드를 반환합니다.
- 2번째는 리스트의 크기 - 1 번째의 노드를 반환합니다.
- 3번째는 다음 리스트의 길이가 0일 경우 노드를 반환하고 아니라면, 다음 리스트에 대해 재귀적으로 수행합니다.
- 4번째는 다음 리스트가 비었을 경우(null값) 노드를 반환하고 아니라면, 다음 리스트에 대해 재귀적으로 수행합니다.
아무래도 간결한 1번째나 두번째 코드가 마음에 들죠? ㅎㅎ
그런데 '()를 입력하면 car나 cdr을 수행할 수 없다는 에러가 뜹니다.
저는 ERROR를 표시하도록 수정하겠습니다.
Code 6.3
(define (last-node list)
(if (null? list)
"ERROR"
(car (reverse list))))
(check-expect (last-node '()) "ERROR")결과: 모든 1개 테스트 통과함!
항상 말하지만 항상 경계값에 대해 테스트하고, 예외처리하는 습관을 들입시다.
본격적으로 자료구조를 배워보도록 합시다!!
2. 자료구조.
- 자료구조의 종류
자료구조는 크게 선형구조와 비선형구조로 나눌수 있으며 다음과 같습니다.
- 선형구조
- 리스트
- 스택
- 큐
- 덱
- 비선형구조
- 트리
- 그래프
위에 나온 데이터구조들을 간단히 알아보고 구현해볼꺼에요.
- 추상 데이터 타입(ADT, Abstract Data Type)
그전에 추상 데이터 타입의 개념에 대해 숙지하고 넘어갑시다.
ADT는 구체적인 구현에 앞서 데이터와 연산의 특징과 연산자가 어떤 기능을 하는지 알려주는 명세입니다.
우리가 지금껏 배워왔던 계약, 목적과 비슷하니 적응하기 쉬울겁니다.
리스트의 ADT
데이터:
- 리스트 형태인 $L$은 요소들이 순서대로 정렬된 것입니다.
$<x_0, x_1, x_2, ... , x_{n-2}, x_{n-1}>$처럼 말이죠. - 리스트의 길이는 $|L|=n$이고, $n=0$일 경우 $L$은 빈 리스트입니다.
- $N$은 노드를 나타냅니다.
연산:
- list-length($L$): $|L|$를 반환합니다.
- list-empty?($L$): 리스트가 비어있는지에 따라 true/false 값을 반환합니다.
- list-get-first($L$): 리스트의 첫번째 요소를 반환합니다.
- list-get-last($L$): 리스트의 마지막 요소를 반환합니다.
- list-get($L$, i): $L[i]$를 반환합니다. 0보다 작거나 $|L|$일 경우, 에러를 반환합니다.
- list-set($L$, i, $N$): $L[i]$을 $N$값으로 바꿈니다.
쉬운 것부터 하나씩 구현해봅시다.
처음 배우는 사람에게 마지막 set부분 코드는 조금 어려울 수 있으니 다 이해하지 못해도 상관없습니다.
리스트와 그 뒤에 나오는 스택, 큐와 같은 자료구조의 개념을 잡는 것이 가장 중요합니다.
구현은 개념 이해를 탄탄히 하기위해 하는 과정일 뿐입니다.
- list-length && list-empty?
Code 6.4
;;list-length: list -> int
;;List's length
(define (list-length lst)
(length lst))
(check-expect (list-length '()) 0)
(check-expect (list-length '(1 2 3 4 5)) 5)
;;list-empty?: list -> boolean
;;Check list is empty
(define (list-empty? lst)
(null? lst))
(check-expect (list-empty? '()) #true )
(check-expect (list-empty? '(1 2 3 4 5)) #false)결과: 모든 4개 테스트 통과함!
list-length와 list-empty는 length와 null?의 사용과 같아 쉽게 만들 수 있다.
- list-get-first && list-get-last
Code 6.4
(define E-list-smaller
"ERROR: index smaller than 0")
(define E-list-larger
"ERROR: index larger than list length")
;;list-get-first: list -> node
;;Return list's first element
(define (list-get-first lst)
(if (null? lst)
E-list-smaller
(car lst)))
(check-expect (list-get-first '()) E-list-smaller)
(check-expect (list-get-first '(1 2 3 4 5)) 1)
;;list-get-last: list -> node
;;Return list's last element
(define (list-get-last lst)
(if (null? lst)
E-list-smaller
(car (reverse lst))))
(check-expect (list-get-last '()) E-list-smaller)
(check-expect (list-get-last '(1 2 3 4 5)) 5)결과: 모든 4개 테스트 통과함!
list-get-first는 car에 예외처리를 더한것 뿐이고, list-get-last는 앞서 만든 last-node와 동일하다.
- list-get
Code 6.4
;;list-get: list index -> node
;;Return list's "index"th element
(define (list-get lst index)
(cond
[(< index 0) E-list-smaller]
[(>= index (length lst)) E-list-larger ]
[else (list-ref lst index)]))
(check-expect (list-get '(1 2 3 4 5) -1) E-list-smaller)
(check-expect (list-get '(1 2 3 4 5) 6) E-list-larger )
(check-expect (list-get '(1 2 3 4 5) 2) 3)결과: 모든 3개 테스트 통과함!
우리가 원하는 값을 잘 알려주고 있습니다.
- list-set
Code 6.4
;;list-set: list index node -> void
;;Set list's "index"th element to node
(define (list-set lst index node)
(append (list-take lst (- index 1))
(list node)
(list-drop lst index)))
;;list-take: list index -> list
;;Split list to"index"th
(define (list-take lst index)
(cond
[(= index 0) '()]
[(< index 0) E-list-smaller]
[(> index (length lst)) E-list-larger ]
[else (cons (car lst)
(list-take (cdr lst) (- index 1)))]))
;;list-drop: list index -> list
;;Split list after "index"th
(define (list-drop lst index)
(cond
[(= index 0) lst ]
[(< index 0) E-list-smaller]
[(> index (length lst)) E-list-larger ]
[else (list-drop (cdr lst) (- index 1))]))
;;(check-expect (list-set '(1 2 3 4 5) 0 10) ERROR)
;;(check-expect (list-set '(1 2 3 4 5) -1 10) ERROR)
;;(check-expect (list-set '(1 2 3 4 5) 6 10) ERROR)
(check-expect (list-set '(1 2 3 4 5) 5 10) '(1 2 3 4 10))
(check-expect (list-take '(1 2 3 4 5) 0 ) '() )
(check-expect (list-take '(1 2 3 4 5) -1) E-list-smaller)
(check-expect (list-take '(1 2 3 4 5) 6 ) E-list-larger )
(check-expect (list-take '(1 2 3 4 5) 5 ) '(1 2 3 4 5))
(check-expect (list-drop '(1 2 3 4 5) 0 ) '(1 2 3 4 5))
(check-expect (list-drop '(1 2 3 4 5) -1) E-list-smaller)
(check-expect (list-drop '(1 2 3 4 5) 6 ) E-list-larger )
(check-expect (list-drop '(1 2 3 4 5) 5 ) '())결과: "ERROR: index smaller than 0" "ERROR: index larger than list length" "ERROR: index smaller than 0" "ERROR: index larger than list length" 모든 9개 테스트 통과함!
index의 앞과 뒷부분의 list를 반환해주는 list-take와 list-drop을 만들었다.
그리고 list-set에서 list-take, node, drop 순으로 새로운 리스트를 만들어 반환해준다.
테스트코드에서 3개를 주석처리해둔 것은 자동으로 에러로 인식해주기 때문이다
2.1 스택(Stack)

쌓여진 상자[from The Cargo Book]
스택은 마치 상자를 사용하는 방법과 같다.
나중에 들어온 것이 먼저 나가는 후입선출(LIFO, Last In First Out)라 불리는 형태의 자료구조이다.
[먼저 들어온 것은 나중에, 나중에 들어온 것은 먼저 나간다]
게임으로 치면 트위치의 패시브 스킬 같은거??
트위치 맹독[from LOL]
스택은 리스트가 있다면 쉽게 구현할 수 있다.

스택[from Wikipedia]
스택의 ADT
데이터:
- 리스트와 동일하다.
리스트의 마지막. 즉, 스택의 윗부분을 TOP이라 부른다.
연산:
- stack-push($L$, $N$): 노드 $N$을 TOP에 추가한다.
- stack-top($L$): TOP을 반환한다.(비어있으면 에러)
- stack-pop($L$): TOP을 제거하고 반환합니다.(역시 비어있으면 에러)
- stack-empty?($L$): 스택이 비었는지 확인합니다.
복잡한 것은 최대한 없애고, 간단하게만 구현하겠습니다.
원래 쓸만하게 짰었는데 초보자에게 어려울거 같아서 다 지워쓔ㅠㅠㅠㅠㅠㅠㅠ
- stack-empty?
Code 6.5
;;stack-empty?: stack -> boolean
;;Check stack is empty
(define (stack-empty? lst)
(null? lst))
(check-expect (stack-empty? '()) #true )
(check-expect (stack-empty? '(1)) #false)결과: 모든 2개 테스트 통과함!
그냥 null값인지만 확인하면 됩니다.
- stack-top && stack-pop
Code 6.5
(define E-stack-empty
"ERROR: stack is empty")
;;stack-top: stack -> node
;;Return stack's TOP
(define (stack-top lst)
(if (stack-empty? lst)
E-stack-empty
(car lst)))
(check-expect (stack-top '()) E-stack-empty)
(check-expect (stack-top '(3 2 1)) 3)
;;stack-pop: stack -> stack
;;Return stack excluding Top
(define (stack-pop lst)
(if (stack-empty? lst)
E-stack-empty
(cdr lst)))
(check-expect (stack-pop '()) E-stack-empty)
(check-expect (stack-pop '(3 2 1)) '(2 1))결과: 모든 4개 테스트 통과함!
stack-top은 스택이 비었는지 확인하고 아니면 car값을 반환해주면 됩니다.
stack-pop은 스택이 비었는지 확인하고 아니면 cdr값을 반환해주면 됩니다.
그냥 리스트 쓰는 거랑 똑같죠?
- stack-push
Code 6.5
;;stack-push: stack node -> stack
;;Return add node to end of list(stack's TOP)
(define (stack-push lst node)
(cons node lst))
(check-expect (stack-push '() 1) '(1))
(check-expect (stack-push (stack-push '() 1) 2) '(2 1))
(check-expect (stack-push '(2 1) 3) '(3 2 1))결과: 모든 3개 테스트 통과함!
노드-리스트 순으로 새로운 리스트를 만들어주면 스택이 됩니다.
쉽죠??
앞서 말했지만 쉽게 만들려고 set!을 이용한 코드 다 갈아 엎었어요ㅠㅠ
스택은 어떨 때 쓰일까요?
재귀에서 1번-2번-3번(종료)-2번-1번처럼 '돌아올때' 쓰일 수 있습니다.
이 말은 괄호 체크 (((예시))), 컨트롤-z(취소하기)등에 쓸 수 있다는 것이겠죠.
2.2 큐(Queue)

냉장고[from carrier]
큐는 스택과 달리 선입선출(FIFO, First In First Out)방식이다.
음식을 저장하는 방식과 같다.
가정에서는 냉장고에 음식을 넣을때 유통기한이나 사온 순서를 생각하지 않고 넣는 경우가 많지만, 마트나 편의점 같은 곳의 냉장고와 진열대를 봐보자.
대부분 유통기한이 짧은 것(먼저 생산된 것)이 앞으로 와있을 것이다.
그냥 버스나 지하철을 타려고 줄을 서는 것이라 생각해도 좋다.

큐[from Wikipedia]
큐의 ADT
데이터:
- 리스트와 동일하다.
큐의 입구를 Back(또는 rear), 출구를 Front라 부른다.
연산:
- queue-enqueue($L$, $N$): 노드 $N$을 Back에 추가한다.
- queue-dequeue($L$): Front를 제거하고 반환합니다.(비어있으면 에러)
- queue-front($L$): Front을 반환한다.(비어있으면 에러)
- queue-empty?($L$): 큐가 비었는지 확인합니다.
스택과 거의 비슷하니 여러분이 구현해보고 코드를 보세요.
- queue-empty?
Code 6.6
;;queue-empty?: queue -> boolean
;;Check queue is empty
(define (queue-empty? lst)
(null? lst))
(check-expect (queue-empty? '()) #true )
(check-expect (queue-empty? '(1)) #false)결과: 모든 2개 테스트 통과함!
- queue-front && queue-dequeue
Code 6.6
(define E-queue-empty
"ERROR: queue is empty")
;;queue-front: queue -> node
;;Return queue's front
(define (queue-front lst)
(if (queue-empty? lst)
E-queue-empty
(car lst)))
(check-expect (queue-front '()) E-queue-empty)
(check-expect (queue-front '(1 2 3)) 1)
;;queue-dequeue: queue -> queue
;;Return queue excluding front
(define (queue-dequeue lst)
(if (queue-empty? lst)
E-queue-empty
(cdr lst)))
(check-expect (queue-dequeue '()) E-queue-empty)
(check-expect (queue-dequeue '(1 2 3)) '(2 3))결과: 모든 4개 테스트 통과함!
- queue-enqueue
Code 6.6
;;queue-enqueue: queue node -> queue
;;Return add node to back
(define (queue-enqueue lst node)
(append lst (list node)))
(check-expect (queue-enqueue '() 1) '(1))
(check-expect (queue-enqueue (queue-enqueue '() 1) 2) '(1 2))
(check-expect (queue-enqueue '(1 2) 3) '(1 2 3))결과: 모든 3개 테스트 통과함!
enqueue때 append를 사용한 것과 순서차이를 빼면 별차이 없죠?
큐는 어떨 때 쓰일까요?
우선순위처럼 '순서대로' 처리할 때 쓰일 수 있습니다.
이 말은 프로세스 관리, 출력 메세지 처리등에 쓸 수 있다는 것이겠죠.
2.3 덱(Deque)

1차선 터널[from 여행이 좋다]
덱(Deque)은 double-ended queue의 약어로서 front와 end에 추가/삭제가 자유롭다.
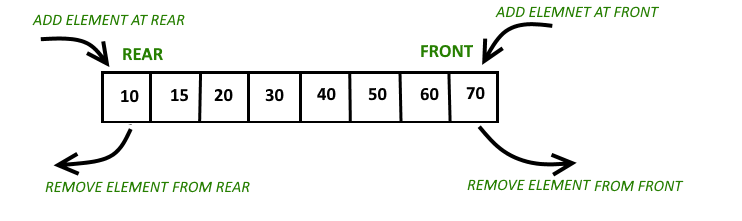
덱[from Geeksforgeeks]
덱의 ADT
데이터:
- 덱과 동일하다.
연산:
- deque-add-front($L$, $N$): 노드 $N$을 front에 추가한다.
- deque-add-back($L$, $N$): 노드 $N$을 back에 추가한다.
- deque-delete-front($L$): Front를 제거하고 반환합니다.(비어있으면 에러)
- deque-delete-back($L$): Back을 제거하고 반환합니다.(비어있으면 에러)
- deque-front($L$): Front을 반환한다.(비어있으면 에러)
- deque-back($L$): Back을 반환한다.(비어있으면 에러)
- deque-empty?($L$): 덱이 비었는지 확인합니다.
- deque-empty?
Code 6.7
;;deque-empty?: deque -> boolean
;;Check deque is empty
(define (deque-empty? lst)
(null? lst))
(check-expect (deque-empty? '()) #true )
(check-expect (deque-empty? '(1)) #false)결과: 모든 2개 테스트 통과함!
- deque-front && deque-back
Code 6.7
(define E-deque-empty
"ERROR: deque is empty")
;;deque-front: deque -> node
;;Return deque's front
(define (deque-front lst)
(if (deque-empty? lst)
E-deque-empty
(car lst)))
(check-expect (deque-front '()) E-deque-empty)
(check-expect (deque-front '(1 2 3)) 1)
;;deque-back: deque -> node
;;Return deque's back
(define (deque-back lst)
(if (deque-empty? lst)
E-deque-empty
(car (reverse lst))))
(check-expect (deque-back '()) E-deque-empty)
(check-expect (deque-back '(1 2 3)) 3)결과: 모든 4개 테스트 통과함!
deque-back은 list-last-node와 같죠?
- deque-delete-front && deque-delete-back
Code 6.7
;;deque-delete-front: deque -> deque
;;Return deque excluding front
(define (deque-delete-front lst)
(if (deque-empty? lst)
E-deque-empty
(cdr lst)))
(check-expect (deque-delete-front '()) E-deque-empty)
(check-expect (deque-delete-front '(1 2 3)) '(2 3))
;;deque-delete-back: deque -> deque
;;Return deque excluding back
(define (deque-delete-back lst)
(if (deque-empty? lst)
E-deque-empty
(list-take lst (- (length lst) 1))))
(check-expect (deque-delete-back '()) E-deque-empty)
(check-expect (deque-delete-back '(1 2 3)) '(1 2))결과: 모든 4개 테스트 통과함!
deque-delete-back은 전에 만들어둔 list-take를 쓰면 됩니다.
예제코드를 보여주는 것이라 가능한 전에 만들었던 함수를 쓰지 않으려 하는데 이 경우는 list-take를 쓰는게 훨씬 이득이라..
- deque-add-front && deque-add-back
Code 6.7
;;deque-add-front: deque node -> deque
;;Return add node to front
(define (deque-add-front lst node)
(append (list node) lst))
(check-expect (deque-add-front '() 1) '(1))
(check-expect (deque-add-front (deque-add-front '() 1) 2) '(2 1))
(check-expect (deque-add-front '(2 1) 3) '(3 2 1))
;;deque-add-back: deque node -> deque
;;Return add node to back
(define (deque-add-back lst node)
(append lst (list node)))
(check-expect (deque-add-back '() 1) '(1))
(check-expect (deque-add-back (deque-add-back '() 1) 2) '(1 2))
(check-expect (deque-add-back '(1 2) 3) '(1 2 3))결과: 모든 6개 테스트 통과함!
노드 삽입 순서가 달라질뿐 거의 차이가 없겠죠?
드디어 선형 자료구조가 끝났습니다!!
생각한 것보다 어렵지 않죠?
비선형 자료구조는 설명할 것이 조금 많습니다 ^^
시작해볼까요?
2.4 트리(Tree)

몬드리안 회색나무[from Wikipedia]
여러 노드가 한 노드를 가리킬 수 없는 구조로 계층적인 데이터를 표현하는데 유리하다.
나무 모양이 보이는지 그림으로 봐보자.
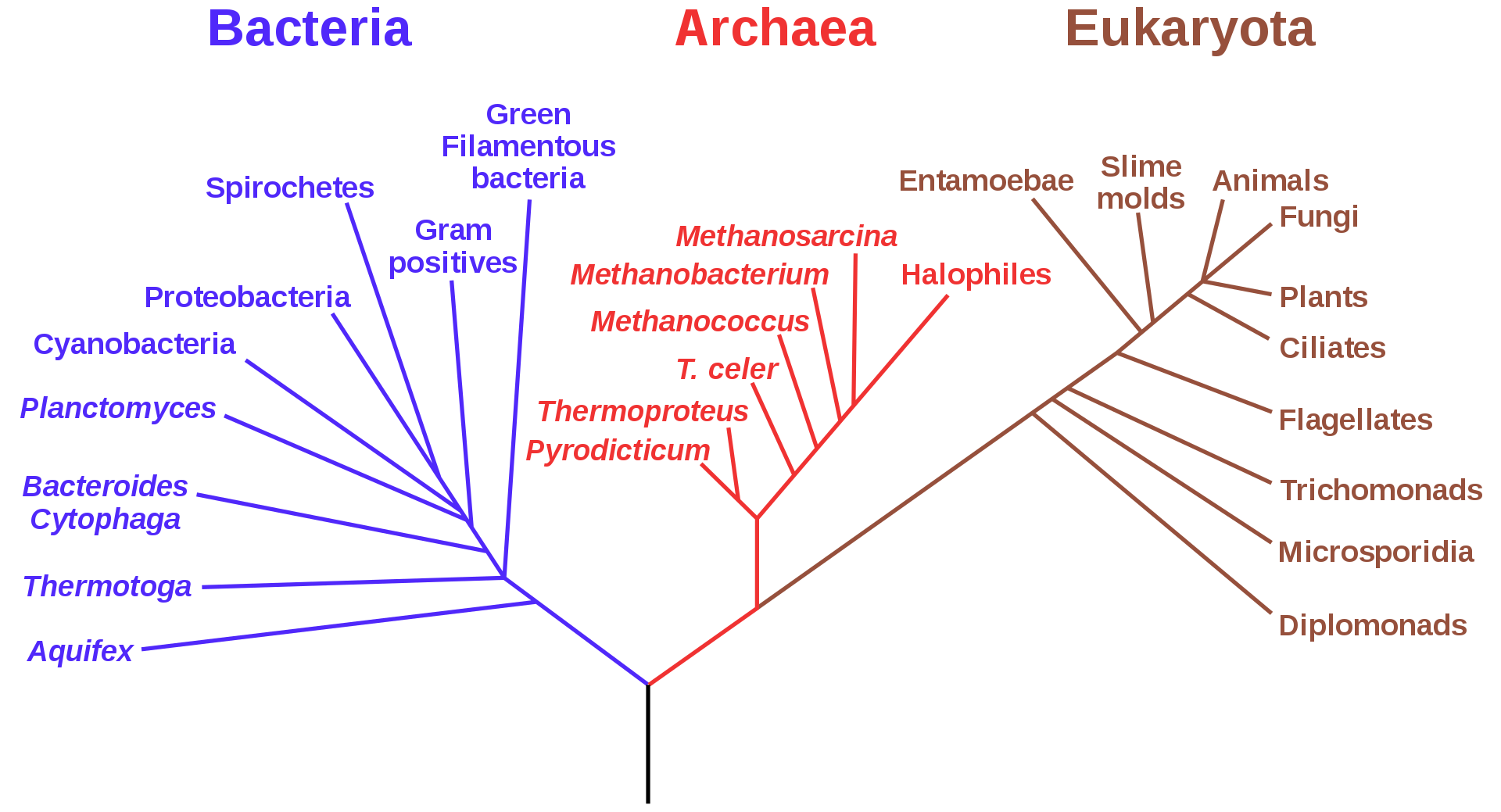
생물 계통 분류[from Wikipedia]
트리는 각 데이터를 나타내는 노드(Node)와 간선(Edge)으로 이루어진다.
트리의 정상에는 한개의 노드가 있고, 이를 루트(Root)라 한다.
트리의 정의
트리는 다음과 같이 재귀적으로 정의할 수 있다.
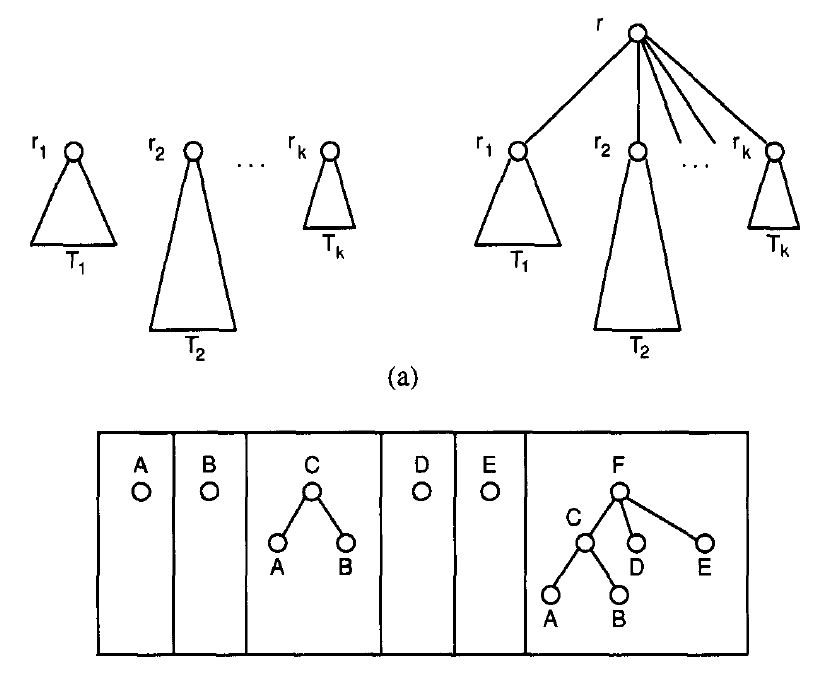
- 간선이 없는 하나의 특별한 노드가 존재하며 트리이다.루트(Root)를 뜻함.
- $T_1, ..., T_k (k \geq 1)$는 공통된 노드가 없는 트리, $r_1, ..., r_k$는 각 트리의 루트며 $r$은 새로운 노드라 가정하자.트리 $T$는 $T_1, ..., T_k$의 노드와 간선, 새로운 노드 $r$와 새로운 간선 $<r,r_1>, ..., <r, r_k>$로 구성된다.$T$의 루트는 $r$이며 $T_1, ..., T_k$는 $T$의 서브트리(Subtree)라 불린다.
트리는 아무래도 구조적으로 복잡하기 때문에 용어도 다양하다.
그 중 중요한 것만 몇개 소개한다.
- 부모(Parent), 자식(Child), 형제(Brother)
트리 정의 그림에서 $C$는 자식 $A$, $B$를 가지고 있는 부모이다.
$A$와 $B$는 형제 노드다. - 말단(Terminal) or 리프(Leaf)
자식이 없는 노드. $A$, $B$, $D$, $E$ 노드가 해당된다. - 깊이(Depth)와 높이(Height)
깊이는 루트로부터 거친 길이. $C$는 2, $A$는 3다.
높이는 가장 긴 깊이. 여기선 3.
트리 중 자식노드를 2개까지만 가질 수 있는 것을 이진트리(Binary Tree)라 부른다.
여러개의 자식을 가지면 다루기가 까다로우므로 이진트리를 사용하는 경우가 많다.
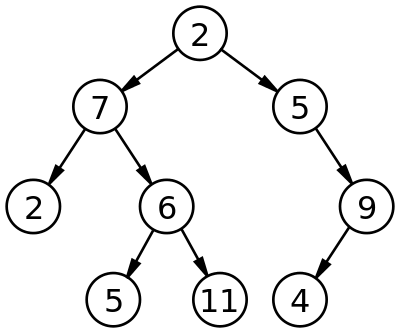
이진트리[from Wikipedia]
트리의 순회
각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정을 말한다.
방식으로는 전위, 중위, 후위, 레벨 순회가 존재한다.
전위, 중위, 후위는 한번 들어본적 있죠?
2018/01/11 - [프로그래밍/설계] - 내 맘대로 프로그램 설계 2. - 데이터 타입.
시간에 Racket이란 언어는 전위 표기법을 이용한 언어라면서
https://black7375.tumblr.com/post/169264990885/전위-중위-후위-표기법
전위, 중위, 후위 표기법.
이글을 제대로 보기위해서는 링크로 들어가시기를 권합니다. 연산자의 위치에 따라 전위, 중위 후위 표기법으로 분류가 된다. 1. 전위 표기법. $$\text{연산자 피연산자 피연산자}$$ 방식으로 표기한다. 일반 폴란드 표기법(NPN), 루카쉐비치 표기법, 바르샤바 표기법, 폴란드 접두사 표기법이라고도 한다. 특징. 쉽게 결정되는 연산순서. 연산자의 순서만...
black7375.tumblr.com
을 소개한 적이 있다. 읽고 오자.
해당 포스트의 연산자와 피연산자를 이진트리 구조로 표현할 수 있다.
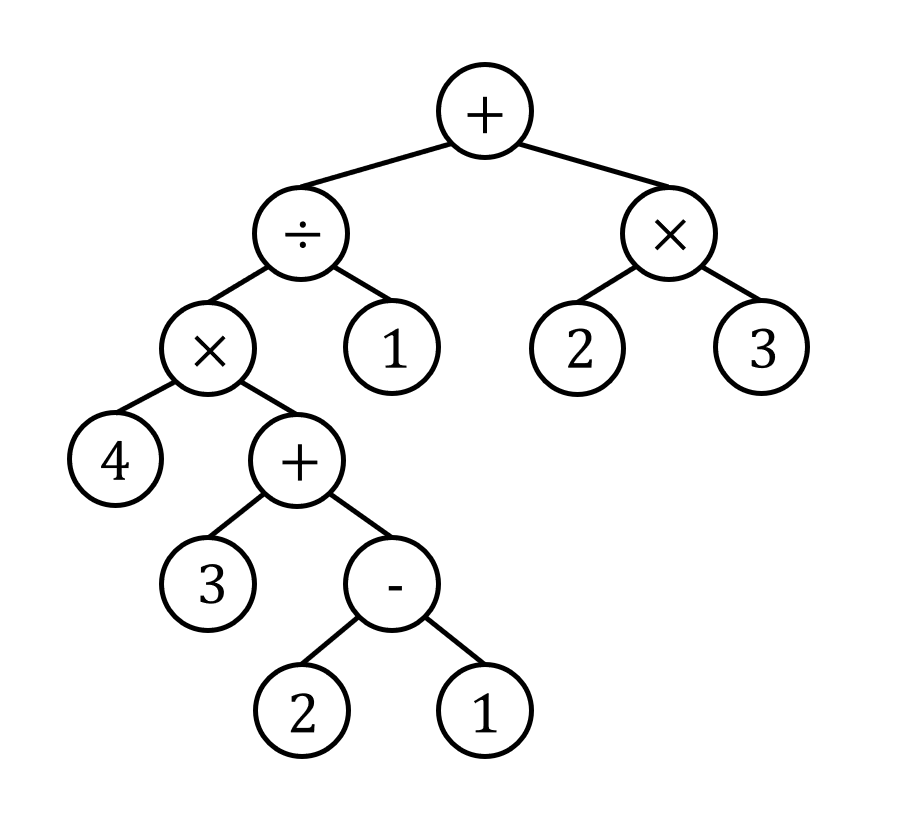
그럼, 전위 중위 후위 순회방식을 그림을 통해 비교해보자.

2에서 1을 빼고 싶다 가정할 때
전위는 $-\; 2\; 1$, 중위는 $2\; -\; 1$ 후위는 $2\; 1\; -$ 방식으로 순회한다.
완전히 같진 않지만.. 삼각함수를 떠올리면 의외로 쉽게 익힐 수 있을 것이다.

전위, 중위, 후위 방식으로 복잡한 트리를 순회해보면 다음과 같이 나타난다.
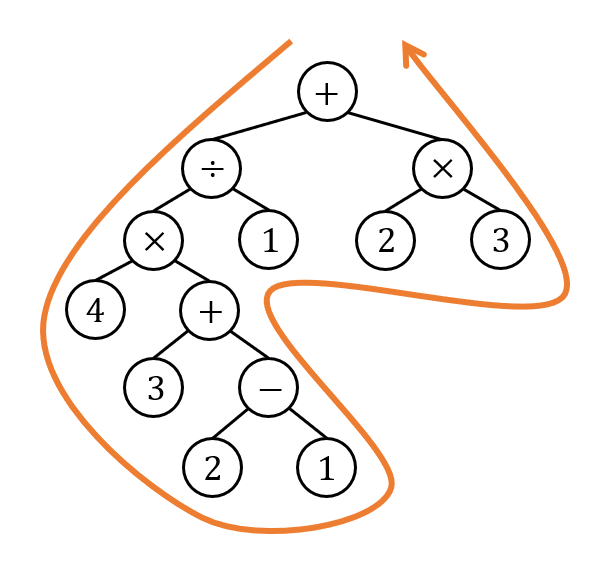


레벨 순회는 높이대로 돌면 된다.

그럼 코드로 트리를 표현해보자.
놀랍게도 달랑 이게 끝이다.
Code 6.8
'(+ (/ (* 4 (+ 3 (- 2 1)))
1)
(* 2 3))
racket은 코드가 데이터, 데이터가 코드가 될 수 있으므로 가능한 일!!
이제 왜 생소한 racket을 강좌 언어로 택했는지 이해가 가길 시작할 것이다.
놀라긴 아직 이르지만 ㅎㅎㅎ
1줄 짜리 리스트의 형태로도 표현이 가능하지만(레벨 순회를 그대로 나타낸 것) 보다시피 공간낭비가 심하고, 직관적이지 않다.
'(+
/ *
* 1 2 3
4 + '() '() '() '() '() '()
'() '() 3 - ...)
+.
참조: Fundamental Data Structures, Data Structures, Data Structures & Their Algorithms(Harry R. Lewis, 1991), Introduction to Algorithms(Thomas H. Cormen, 2013)